Zufallsvariablen in der Statistik

Die Welt ist voller Unsicherheiten, und Mathematik bietet uns Werkzeuge, um diese zu verstehen und vorherzusagen. Eine zentrale Rolle in diesem Kontext spielt die Zufallsvariable, ein Konzept aus der Wahrscheinlichkeitstheorie. Doch was genau ist eine Zufallsvariable, warum ist sie wichtig, und wie können wir sie verwenden?

Grundlegendes Verständnis einer Zufallsvariable

Eine Zufallsvariable ist eine Funktion, die möglichen Ergebnissen eines Zufallsexperiments Zahlen zuordnet. Dies ermöglicht es uns, Zufallsprozesse zu quantifizieren und mathematisch zu analysieren.

Formale Definition

Eine Zufallsvariable $X$ ist eine Funktion, die jedem Element $\omega$ (kleines Omega) eines Ereignisraums $\Omega$ (großes Omega) eine reelle Zahl zuweist:

$$X: \Omega \to \mathbb{R}$$

Hierbei steht:

• $\Omega$: der Ereignisraum, also die Menge aller möglichen Ergebnisse eines Zufallsexperiments.
• $X(\omega)$: der Wert der Zufallsvariable für ein bestimmtes Ergebnis $\omega$.

Ein Beispiel hilft, diese abstrakte Definition zu verdeutlichen.

Beispiel: Würfeln

Stellen die vor, du wirfst einen Würfel:

• Der Ereignisraum $\Omega$ enthält alle möglichen Ergebnisse: $\{1, 2, 3, 4, 5, 6\}$.
• Eine mögliche Zufallsvariable könnte die gewürfelte Augenzahl darstellen, also: $X(\omega) = \omega, \, \text{wobei } \omega \in \{1, 2, 3, 4, 5, 6\}$.

In diesem Fall entspricht der Wert der Zufallsvariable $X$ direkt dem Ergebnis des Würfels.

Arten von Zufallsvariablen

Zufallsvariablen lassen sich grob in zwei Kategorien einteilen: diskrete und stetige Zufallsvariablen.

1. Diskrete Zufallsvariablen

Eine Zufallsvariable heißt diskret, wenn sie nur endlich viele oder abzählbar unendlich viele Werte annehmen kann.

Eigenschaften

• Die Werte sind klar voneinander getrennt.
• Die Wahrscheinlichkeit, dass eine bestimmte Zahl angenommen wird, kann durch eine Wahrscheinlichkeitsmassenfunktion beschrieben werden: $P(X = x)$.

Beispiele

1. Würfeln: Die Augenzahlen (1 bis 6) sind diskrete Werte.
2. Anzahl der Kunden: In einem Geschäft kommen täglich 0, 1, 2, … Kunden.

2. Stetige Zufallsvariablen

Eine Zufallsvariable heißt stetig, wenn sie jeden Wert in einem Intervall annehmen kann.

Eigenschaften

• Zwischen zwei Werten gibt es unendlich viele weitere mögliche Werte.
• Wahrscheinlichkeiten werden über eine Wahrscheinlichkeitsdichtefunktion definiert. Die Wahrscheinlichkeit, dass die Zufallsvariable genau einen bestimmten Wert annimmt, ist theoretisch null. Stattdessen betrachtet man Wahrscheinlichkeiten für Intervalle.

Beispiele

1. Körpergröße: Eine Person kann 170,5 cm oder 170,503 cm groß sein.
2. Zeit bis zum Ausfall eines Geräts: Die Zeitspanne ist kontinuierlich.

Warum sind Zufallsvariablen wichtig?

Zufallsvariablen sind das Herzstück vieler Anwendungsbereiche der Statistik und Wahrscheinlichkeit. Sie bieten eine Möglichkeit, reale Phänomene mathematisch zu modellieren und vorherzusagen. Hier sind einige wichtige Gründe, warum sie so zentral sind:

1. Quantifizierung von Unsicherheiten: Zufallsvariablen ermöglichen es, Unsicherheiten zu messen und zu analysieren.
2. Mathematische Modellierung: Sie helfen, komplexe Prozesse wie Wetter, Aktienkurse oder genetische Vererbung mathematisch zu beschreiben.
3. Grundlage für Wahrscheinlichkeitsverteilungen: Jede Zufallsvariable hat eine Verteilung, die zeigt, wie wahrscheinlich verschiedene Ergebnisse sind.
4. Entscheidungsfindung: In Bereichen wie Versicherungsmathematik, Finanzwesen und Risikomanagement sind Zufallsvariablen unverzichtbar.

Verteilung von Zufallsvariablen

Die Verteilung einer Zufallsvariable beschreibt, wie die Wahrscheinlichkeiten über die möglichen Werte verteilt sind. Es gibt unterschiedliche Arten von Verteilungen, die sich je nach Art der Zufallsvariablen unterscheiden.

Diskrete Verteilung

Bei diskreten Zufallsvariablen wird die Wahrscheinlichkeitsverteilung durch die Wahrscheinlichkeitsmassenfunktion (PMF) beschrieben. Diese Funktion gibt an, mit welcher Wahrscheinlichkeit $P(X = x)$ die Zufallsvariable $X$ den Wert $x$ annimmt.

Beispiel: Münzwurf

• Ereignisraum: $\{Kopf, Zahl\}$
• Zufallsvariable: $X = \begin{cases} 1, & \text{wenn Kopf}, \\ 0, & \text{wenn Zahl}. \end{cases}$

Die Wahrscheinlichkeiten sind:$P(X = 1) = 0,5 \quad \text{und} \quad P(X = 0) = 0,5$.

Stetige Verteilung

Bei stetigen Zufallsvariablen wird die Verteilung durch die Wahrscheinlichkeitsdichtefunktion (PDF) beschrieben. Die Wahrscheinlichkeit, dass die Zufallsvariable einen Wert in einem Intervall annimmt, wird durch das Integral der Dichtefunktion berechnet: $P(a \leq X \leq b) = \int_a^b f_X(x) \, dx$

Beispiel: Körpergröße

• Ereignisraum: Alle Werte in einem Intervall, z. B. $[150,200]$
• Wahrscheinlichkeitsdichte: Eine Normalverteilung könnte die Wahrscheinlichkeiten für verschiedene Körpergrößen beschreiben.

Mathematische Eigenschaften von Zufallsvariablen

1. Erwartungswert

Der Erwartungswert (oder Mittelwert) einer Zufallsvariable gibt an, welchen Wert wir im Durchschnitt erwarten können, wenn wir das Experiment unendlich oft wiederholen.

• Diskret: $E(X) = \sum_x x \cdot P(X = x)$
• Stetig: $E(X) = \int_{-\infty}^{\infty} x \cdot f_X(x) \, dx$

2. Varianz

Die Varianz misst, wie stark die Werte einer Zufallsvariable um den Erwartungswert streuen:

$$\text{Var}(X) = E((X – E(X))^2)$$

3. Standardabweichung

Die Standardabweichung ist die Wurzel der Varianz und gibt die durchschnittliche Abweichung vom Mittelwert an.

$$\text{SD}(X) = \sqrt{\text{Var}(X)}$$

Visualisierung von Zufallsvariablen

Diagramme und Grafiken helfen, das Verhalten von Zufallsvariablen zu verstehen. Hier sind einige gebräuchliche Visualisierungen:

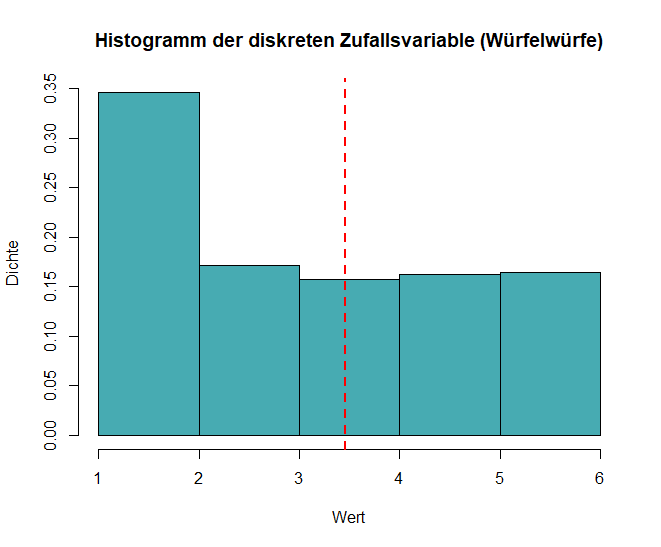
Histogramme: Zeigen die Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen (siehe Beispiel-Code in R unten):

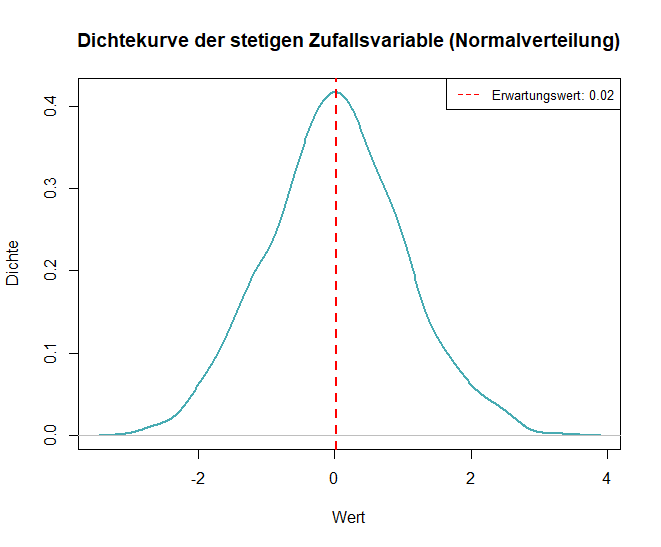
Dichtekurven: Veranschaulichen die Wahrscheinlichkeitsdichte von stetigen Zufallsvariablen (siehe Beispiel-Code in R unten):

Zusammenfassendes Beispiel in R

# Diskrete Zufallsvariable (z.B. Würfelwürfe)
set.seed(123)
dice_rolls <- sample(1:6, size = 1000, replace = TRUE)

# Erwartungswert, Varianz und Standardabweichung für die diskrete Zufallsvariable
mean_discrete <- mean(dice_rolls)
var_discrete <- var(dice_rolls)
sd_discrete <- sd(dice_rolls)

# Stetige Zufallsvariable (z.B. Normalverteilung)
set.seed(123)
continuous_data <- rnorm(1000, mean = 0, sd = 1)

# Erwartungswert, Varianz und Standardabweichung für die stetige Zufallsvariable
mean_continuous <- mean(continuous_data)
var_continuous <- var(continuous_data)
sd_continuous <- sd(continuous_data)

# Histogramm für die diskrete Zufallsvariable
hist(dice_rolls, breaks = 6, probability = TRUE, col = "#47abb2",
     main = "Histogramm der diskreten Zufallsvariable (Würfelwürfe)",
     xlab = "Wert", ylab = "Dichte")
abline(v = mean_discrete, col = "red", lwd = 2, lty = 2)
legend("topright", legend = paste("Erwartungswert:", round(mean_discrete, 2)), col = "red", lty = 2, cex = 0.8)

# Dichtekurve für die stetige Zufallsvariable
plot(density(continuous_data), col = "#47abb2", lwd = 2,
     main = "Dichtekurve der stetigen Zufallsvariable (Normalverteilung)",
     xlab = "Wert", ylab = "Dichte")
abline(v = mean_continuous, col = "red", lwd = 2, lty = 2)
legend("topright", legend = paste("Erwartungswert:", round(mean_continuous, 2)), col = "red", lty = 2, cex = 0.8)