Der Pearson-Korrelationskoeffizient, benannt nach Karl Pearson, ist ein statistisches Maß, das die lineare Beziehung zwischen zwei metrischen Variablen quantifiziert. Hier sehen wir uns näher an, wie du ihn berechnest und interpretierst.
Definition und Interpretation des Pearson-Koeffizienten
Die Formel für den Pearson-Korrelationskoeffizienten lautet:
$$r = \frac{\sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum_{i=1}^n (x_i – \bar{x})^2 \sum_{i=1}^n (y_i – \bar{y})^2}}$$
Dabei bedeuten:
- $x_i$, $y_i$: Die einzelnen Werte der beiden Variablen $X$ und $Y$.
- $\overline{x}$, $\overline{y}$: Die Mittelwerte von $X$ und $Y$.
- $n$: Die Anzahl der Paare.
Interpretation des Korrelationskoeffizienten
Der Wertebereich von $r$ liegt zwischen -1 und +1:
- +1: Perfekte positive Korrelation (wenn eine Variable steigt, steigt die andere proportional).
- 0: Keine lineare Korrelation (kein linearer Zusammenhang zwischen den Variablen).
- -1: Perfekte negative Korrelation (wenn eine Variable steigt, sinkt die andere proportional).
Die Stärke des Zusammenhangs wird oft wie folgt interpretiert:
| Korrelationskoeffizient ($r$) | Stärke des Zusammenhangs |
|---|---|
| 0.0 bis 0.2 | Sehr schwach |
| 0.2 bis 0.4 | Schwach |
| 0.4 bis 0.6 | Mittel |
| 0.6 bis 0.8 | Stark |
| 0.8 bis 1.0 | Sehr stark |
Manchmal ist es in der Statistik notwendig, Variablen vor des eigentlichen Hypothesentests zu transformieren. Das ist auch nicht weiter schlimm – das Ergebnis der Korrelation wird sich dadurch (bis auch evt. das Vorzeichen) nicht ändern, solange es sich um eine lineare Transformation handelt. Das wird auch als die Maßstabsunabhängigkeit von $r$ bezeichnet.
Visualisierung von Zusammenhängen
Um den Zusammenhang zwischen zwei Variablen besser zu verstehen, eignen sich Streudiagramme. Ein Beispiel für ein stark positives Streudiagramm zeigt, wie die Punkte nahe an einer aufsteigenden Linie liegen.
Voraussetzungen für die Anwendung
Um den Pearson-Korrelationskoeffizienten sinnvoll anwenden zu können, sollten folgende Bedingungen erfüllt sein:
Metrische Skalenniveaus: Beide Variablen müssen metrisch skaliert sein. Das weißt du entweder basierend darauf, wie die Daten definiert sind oder weil sie empirisch „danach aussehen“ (z.B. Kommastellen, es gibt viele unterschiedliche Ausprägungen, etc.). Ist eine der Variablen nur ordinal skaliert, solltest du auf eine Rangkorrelation wechseln.
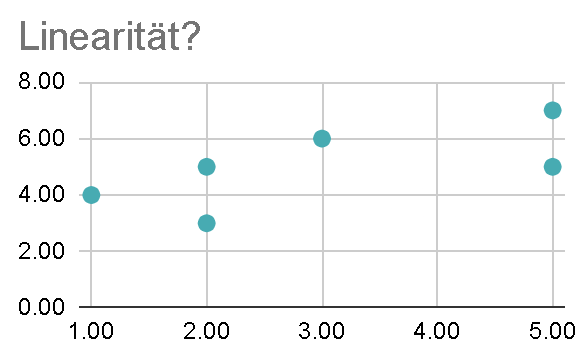
Lineare Beziehung: Der Zusammenhang sollte annähernd linear sein. Das kannst du überprüfen, indem du dir einen Scatterplot ansiehst. Kannst du dir hier eine Gerade vorstellen, die die Punktwolke halbwegs gut zusammenfasst? Was wir jedenfalls nicht sehen wollen ist ein (umgedrehtes) U: das wäre eine nicht-lineare Beziehung!
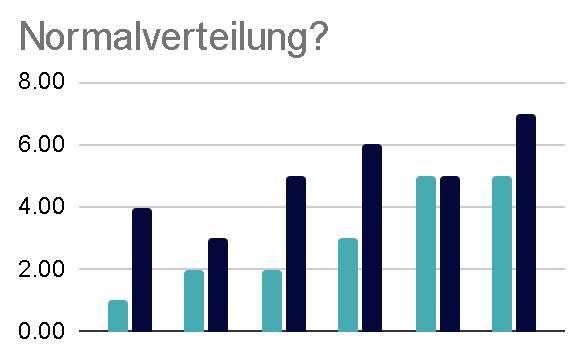
Normalverteilung: Beide Variablen sollten annähernd normalverteilt sein. Wenn das nicht der Fall ist, bietet sich eventuell Spearmans‘ Rangkorrelation als Alternative an. Auch ier bietet sich eine visuelle Analyse der Histogramme an. Wenn du es genau wissen willst, gibt es natürlich auch statistische Tests darüber, z.B. den Shapiro-Wilk Test.
Keine Ausreißer: Extremwerte können den Korrelationswert stark beeinflussen.
Kritische Werte der Korrelation ($\alpha = 0.05$)
Um die statistische Signifikanz des Hypothesentests zu schätzen, können wir auf eine Tabelle mit kritischen Werten als Vergleich zurückgreifen. Wichtig ist dabei insbesonder die Fallzahl $n$, die bestimmt, in welcher Zeile wir in der Tabelle nachsehen müssen. Sehen wir dann ein $r$, dass dem kritischen Wert (in der entsprechenden Zeile) mindestens entspricht (Achtung, es handelt sich um absolute Zahlen!) können wir von statististischer Signifikant ($p < 0.05$) ausgehen.
| Freiheitsgrade: n – 2 | (absolute) Kritische Werte |
|---|---|
| 1 | 0.997 |
| 2 | 0.950 |
| 3 | 0.878 |
| 4 | 0.811 |
| 5 | 0.754 |
| 6 | 0.707 |
| 7 | 0.666 |
| 8 | 0.632 |
| 9 | 0.602 |
| 10 | 0.576 |
| 11 | 0.555 |
| 12 | 0.532 |
| 13 | 0.514 |
| 14 | 0.497 |
| 15 | 0.482 |
| 16 | 0.468 |
| 17 | 0.456 |
| 18 | 0.444 |
| 19 | 0.433 |
| 20 | 0.423 |
| 21 | 0.413 |
| 22 | 0.404 |
| 23 | 0.396 |
| 24 | 0.388 |
| 25 | 0.381 |
| 26 | 0.374 |
| 27 | 0.367 |
| 28 | 0.361 |
| 29 | 0.355 |
| 30 | 0.349 |
| 40 | 0.304 |
| 50 | 0.273 |
| 60 | 0.250 |
| 70 | 0.232 |
| 80 | 0.217 |
| 90 | 0.205 |
| 100 | 0.195 |
Beispiel: Untersuchung eines Zusammenhangs
Stell dir vor, du möchtest den Zusammenhang zwischen der Lernzeit (in Stunden) und der Punktzahl in einem Test untersuchen. Für sechs Studierende liegen folgende Werte vor:
| Studierende | Lernzeit (Stunden) $X$ | Testpunktzahl $Y$ |
|---|---|---|
| A | 2 | 50 |
| B | 3 | 60 |
| C | 5 | 80 |
| D | 4 | 70 |
| E | 6 | 90 |
| F | 1 | 40 |
Hier findest du die Berechnung in Google Sheets:
Einschränkungen und Vorsicht bei der Interpretation
- Korrelation ist keine Kausalität: Auch wenn zwei Variablen korrelieren, bedeutet dies nicht, dass die eine die andere verursacht.
- Nur lineare Zusammenhänge: Der Pearson-Koeffizient misst ausschließlich lineare Zusammenhänge. Nicht-lineare Zusammenhänge werden nicht erfasst.
- Einfluss von Ausreißen: Einzelne extreme Werte können den Wert von \$r\$ stark verzerren.
Anwendungsfelder des Pearson-Koeffizienten
Der Pearson-Korrelationskoeffizient findet Anwendung in vielen Bereichen, darunter (beispielshaft):
- Psychologie: Zusammenhang zwischen Intelligenzquotient und schulischen Leistungen.
- Medizin: Beziehung zwischen Dosis eines Medikaments und der Wirkung.
- Wirtschaft: Zusammenhang zwischen Marketing-Ausgaben und Umsatz.
Fazit
Der Pearson-Korrelationskoeffizient ist ein wertvolles Werkzeug zur Analyse linearer Zusammenhänge zwischen zwei Variablen. Seine Anwendung erfordert jedoch Sorgfalt, insbesondere in Bezug auf die Voraussetzungen und die Interpretation der Ergebnisse. Mit geeigneten Visualisierungen und ergänzenden Maßen kann er jedoch tiefere Einblicke in die Daten liefern.
