Die Visualisierung von Daten ist ein zentraler Bestandteil der statistischen Analyse. Sie hilft dabei, komplexe Zusammenhänge auf einfache Weise zu präsentieren und Muster oder Auffälligkeiten in den Daten zu erkennen. Besonders im Zeitalter der Datenwissenschaft ist die Fähigkeit, Daten effektiv zu visualisieren, ein wertvolles Werkzeug. In diesem Beitrag gehen wir auf einige der wichtigsten Techniken zur Visualisierung statistischer Daten ein und zeigen, wie man diese in R umsetzt.
Warum ist Visualisierung wichtig?
Visualisierungen bieten einen schnellen Zugang zu den Daten, indem sie es uns ermöglichen, Trends, Verteilungen oder Ausreißer sofort zu erkennen. Dadurch kann man Hypothesen aufstellen oder überprüfen, bevor man tiefere statistische Analysen durchführt.
Pinzipien der Datenvisualisierung
Viele Wissenschaftlerinnen und Wissenschaftler sind nicht ausreichend in Gestaltungsprinzipien geschult, um ihre Botschaften visuell optimal zu vermitteln. Dabei sind effektive Figuren nicht nur ein Nebenprodukt wissenschaftlicher Arbeiten, sondern entscheidend für die Vermittlung der Kernaussagen.
Gute Visualisierungen erfordern Planung, bewusste Entscheidungen und ein grundlegendes Verständnis von Designprinzipien. Der Artikel The Bigger Picture (Midway, Stephen R., Patterns, Volume 1, Issue 9) stellt Prinzipien vor, die helfen können, wissenschaftliche Visualisierungen wirkungsvoller und klarer zu gestalten.
Prinzip 1: Planung vor der Gestaltung
Der erste und vielleicht wichtigste Schritt ist, die zentrale Botschaft der Visualisierung zu klären, bevor mit der Erstellung begonnen wird. Die Frage lautet: Welches Ziel verfolgt die Figur? Soll sie einen Vergleich zeigen, eine Beziehung verdeutlichen oder Daten verteilen? Erst wenn diese Botschaft klar ist, sollte die Visualisierung entworfen werden – idealerweise zunächst mit Stift und Papier, um nicht von den Einschränkungen einer Software beeinflusst zu werden.
Prinzip 2: Die richtige Software und die passenden Geometrien
Effektive Visualisierungen erfordern den Einsatz geeigneter Software. Oft reicht ein einfaches Tabellenkalkulationsprogramm nicht aus, um komplexe und ansprechende Visuals zu erstellen. Wissenschaftler müssen bereit sein, neue Tools zu erlernen oder bestehende Fähigkeiten zu erweitern. Gleichzeitig ist es entscheidend, die richtige geometrische Darstellung zu wählen – sei es ein Scatterplot, ein Histogramm oder ein Boxplot. Jede Geometrie hat ihre Stärken und Schwächen, und ihre Auswahl sollte auf der Botschaft der Visualisierung basieren.
Prinzip 3: Farben gezielt einsetzen
Farben sind ein mächtiges Werkzeug in der Visualisierung, doch sie müssen mit Bedacht eingesetzt werden. Farben vermitteln Informationen, ob direkt oder subtil, und beeinflussen die Wahrnehmung von Daten. Dabei sollte immer darauf geachtet werden, dass Figuren auch in Graustufen verständlich bleiben und für farbenblinde Leser geeignet sind. Tools wie ColorBrewer können helfen, geeignete Farbschemata auszuwählen.
Prinzip 4: Unsicherheiten sichtbar machen
Ein häufiger Fehler in wissenschaftlichen Visualisierungen ist das Fehlen von Unsicherheitsangaben. Ob durch Konfidenzintervalle, Fehlerbalken oder andere Darstellungen – Unsicherheiten sollten klar kommuniziert werden, um Missverständnisse zu vermeiden. Wissenschaftliche Visualisierungen leben davon, sowohl die Daten als auch ihre Grenzen transparent darzustellen.
Prinzip 5: Einfachheit und Details im Gleichgewicht
Eine gelungene Figur ist oft einfach im Design, aber reich an Details in der Beschreibung. Die dazugehörigen Bildunterschriften sollten so umfassend sein, dass die Figur auch ohne den restlichen Text verstanden werden kann. Gleichzeitig sollten überflüssige Designelemente, sogenannte „Chartjunk“, vermieden werden, um die Kernbotschaft nicht zu verwässern.
Prinzip 6: Feedback und Weiterentwicklung
Niemand sieht die Schwächen einer Figur so gut wie Außenstehende. Deshalb ist es ratsam, Feedback von Kolleginnen und Kollegen einzuholen – idealerweise nur zur Figur, ohne den begleitenden Text. So wird sichergestellt, dass die Visualisierung eigenständig funktioniert und klar verständlich ist.
Exemplarische Darstellungsformen
Säulendiagramme und Balkendiagramme
Säulen- oder Balkendiagramme eignen sich hervorragend zur Darstellung von kategorialen Daten. Sie ermöglichen es, die Häufigkeit oder den Anteil von Kategorien auf einfache Weise zu vergleichen. Ein Säulendiagramm zeigt die Kategorien auf der x-Achse und die Häufigkeiten auf der y-Achse.
Beispiel: Säulendiagramm in R
# Beispiel: Säulendiagramm
library(ggplot2)
# Datenset: Anzahl Zimmer und Häufigkeit
zimmer <- data.frame(
Kategorie = c("1 Zimmer", "2 Zimmer", "3 Zimmer", "4 Zimmer"),
Häufigkeit = c(50, 120, 200, 80)
)
# Plot erstellen
ggplot(zimmer, aes(x = Kategorie, y = Häufigkeit)) +
geom_bar(stat = "identity", fill = "lightblue") +
ggtitle("Anzahl der Wohnungen nach Zimmeranzahl") +
theme_minimal()
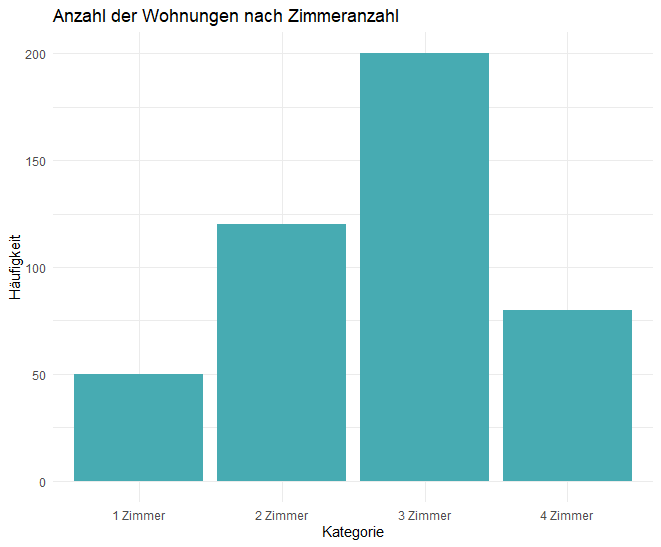
In diesem Beispiel wird die Anzahl von Wohnungen mit unterschiedlichen Zimmern in einem Balkendiagramm dargestellt. Dies ist ein einfacher, aber effektiver Weg, um kategoriale Daten zu visualisieren.
Histogramme
Für stetige Daten eignet sich das Histogramm. Es zeigt, wie sich Werte über verschiedene Intervalle verteilen. Das Buch hebt die Bedeutung von Histogrammen hervor, um Verteilungen auf einfache Weise darzustellen.
Beispiel: Histogramm in R
# Beispiel: Histogramm
set.seed(123) # Für Reproduzierbarkeit
daten <- rnorm(1000, mean = 50, sd = 10) # Beispielhafte Normalverteilung
# Plot erstellen
ggplot(data.frame(daten), aes(x = daten)) +
geom_histogram(binwidth = 2, color = "black", fill = "lightblue") +
ggtitle("Histogramm der Verteilung") +
theme_minimal()
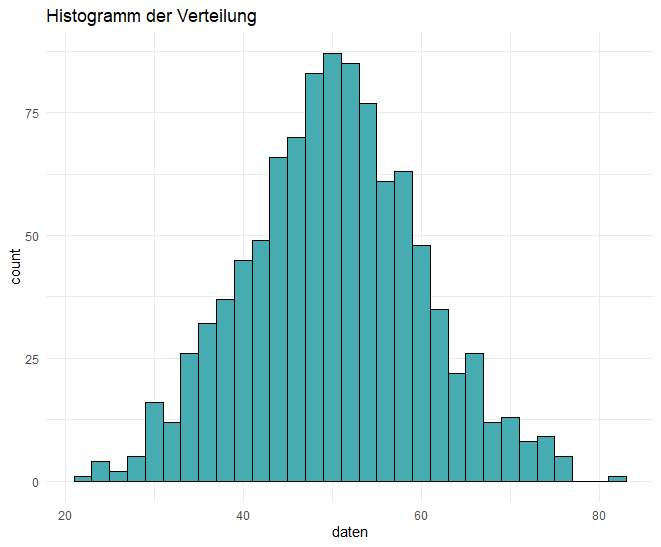
Hier haben wir eine normalverteilte Zufallsvariable, deren Verteilung mit einem Histogramm visualisiert wird. Die Verteilung kann sofort erfasst und auf Normalität geprüft werden.
Boxplots
Ein Boxplot ist ein weiteres nützliches Werkzeug zur Darstellung von Verteilungen, insbesondere wenn man mehrere Gruppen miteinander vergleichen möchte. Ein Boxplot zeigt die Spannweite, den Median und mögliche Ausreißer der Daten.
Beispiel: Boxplot in R
# Beispiel: Boxplot
daten_zimmer <- data.frame(
Zimmer = factor(rep(c("1 Zimmer", "2 Zimmer", "3 Zimmer", "4 Zimmer"), each = 100)),
Miete = c(rnorm(100, mean = 500, sd = 50),
rnorm(100, mean = 700, sd = 70),
rnorm(100, mean = 900, sd = 80),
rnorm(100, mean = 1200, sd = 100))
)
# Boxplot erstellen
ggplot(daten_zimmer, aes(x = Zimmer, y = Miete)) +
geom_boxplot(fill = "#47abb2") +
ggtitle("Nettomiete pro Zimmeranzahl") +
theme_minimal()
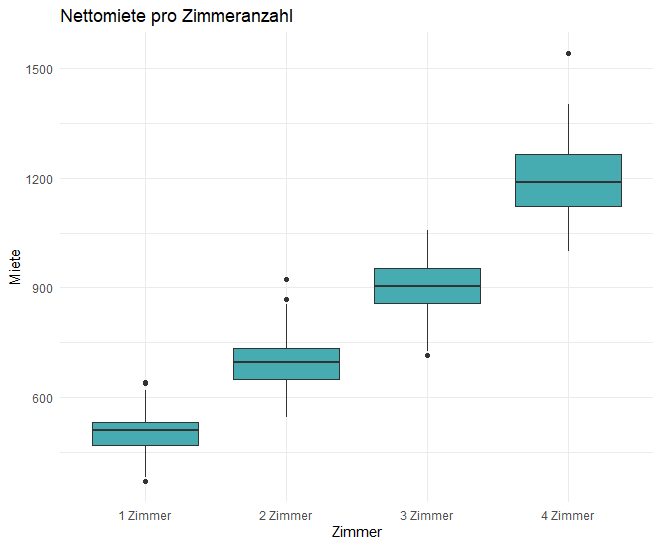
Mit diesem Boxplot vergleichen wir die Verteilung der Nettomiete in Abhängigkeit von der Anzahl der Zimmer. Boxplots sind nützlich, um Unterschiede in den Verteilungen der einzelnen Gruppen zu erkennen.
Streudiagramme
Das Streudiagramm ist ideal, um den Zusammenhang zwischen zwei metrischen Variablen darzustellen. Auf den Seiten 42 bis 43 des Buches wird das Streudiagramm als unverzichtbares Tool für die Exploration von Zusammenhängen hervorgehoben.
Beispiel: Streudiagramm in R
# Beispiel: Streudiagramm
daten_fläche_miete <- data.frame(
Wohnfläche = rnorm(100, mean = 70, sd = 15),
Nettomiete = rnorm(100, mean = 900, sd = 200)
)
# Streudiagramm erstellen
ggplot(daten_fläche_miete, aes(x = Wohnfläche, y = Nettomiete)) +
geom_point(color = "blue") +
ggtitle("Zusammenhang zwischen Wohnfläche und Nettomiete") +
theme_minimal()
Das Streudiagramm zeigt den Zusammenhang zwischen der Wohnfläche und der Nettomiete. Dies ist besonders nützlich, um zu prüfen, ob ein linearer Zusammenhang besteht oder ob andere Muster in den Daten erkennbar sind.
Visuelles Storytelling
Diese exemplarische Auflistung von Darstellungsmöglichkeiten ist tatsächlich sehr kurz und in gewisse Weise ungenügend. Durch die hohe Prävalenz von Daten im Alltag, wird es umso wichtiger, Darstellungen und weitere Überlegungen (wie z.B. die eigentliche Story, die dahinter steht) intensiver zu verknüpfen.
Zum Beispiel entwickeln Zhang et al. (2022, A visual data storytelling framework. Informatics, 9(4), 73. https://doi.org/10.3390/informatics9040073) in ihrer Arbeit ein innovatives Rahmenwerk, das visuelles Datenstorytelling mit narrativen und unterhaltsamen Elementen kombiniert. Ziel ist es, Daten nicht nur informativ, sondern auch zugänglich und ansprechend zu präsentieren. Mithilfe eines modularen Ansatzes, der auf Informationsstrukturierung, technologischer Integration und kognitiven Faktoren basiert, wird die traditionelle Datenvisualisierung durch interaktive und storybasierte Formate erweitert. Die Autoren demonstrieren dies anhand eines Prototyps, der die Einbindung von narrativen Einheiten in interaktive Datenpräsentationen veranschaulicht. Dieser Ansatz bietet neue Möglichkeiten, komplexe Daten einem breiten Publikum verständlich zu machen und sie in handlungsrelevante Erkenntnisse zu übersetzen.
Fazit
Die Visualisierung ist ein unverzichtbarer Teil der Datenanalyse. Sie hilft uns, Muster in den Daten zu erkennen, Hypothesen aufzustellen und Ergebnisse zu kommunizieren. Die in diesem Beitrag vorgestellten Methoden sind nur ein kleiner Ausschnitt aus den vielfältigen Möglichkeiten, die uns R bietet, um Daten grafisch darzustellen. Die auf den Seiten 37 bis 45 des Buches beschriebenen Visualisierungstechniken bieten einen hervorragenden Einstieg, und die hier gezeigten Beispiele kannst du leicht auf deine eigenen Datensätze anwenden.
